Epoch of Reionization data
Here you can find compilations of observational data from the Epoch of Reionization.
Radio-loud quasars at \(z>5.5\) - currently 34 confirmed
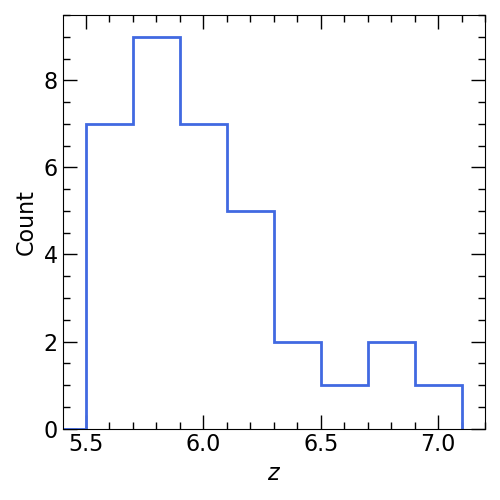
Left: Redshift distribution of \(z>5.5\) radio-loud quasars. All of these radio-loud quasars and some information about them (name, redshift, intrinsic flux density at \(147\,\rm MHz\), spectral index between \(1.4\,\rm GHz\) and \(147\,\rm MHz\), references) are listed in the table above. An excel spreadsheet containing this information can be downloaded here.
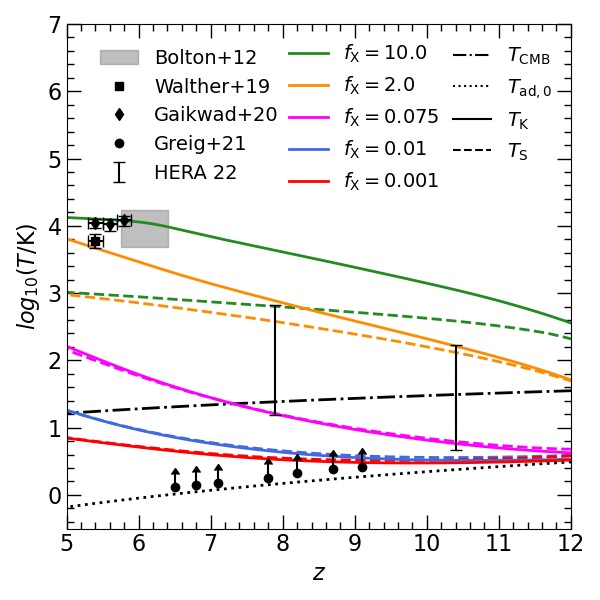
Right: Temperature evolution at mean density for different X-ray background radiation efficiency, \(f_{\rm X}\), and comparison with observational data (listed below, excel spreadsheet here). The computation of this is described in the Appendix B of Šoltinský et al. 2021. Hence, if you find this useful, please consider citing this paper.
Temperature measurements at \(z\geq5\)
| \(z\) | \(T(\rm gas\, kinetic)/\rm K\) | \(T(\rm spin)/\rm K\) | Method | Reference |
|---|---|---|---|---|
| \(10.4\) | \(3.2-313.2\) | \(4.7-171.2\) | 21-cm power spectrum | HERA 2023 |
| \(7.9\) | \(13.0-4768.0\) | \(15.6-656.7\) | 21-cm power spectrum | HERA 2023 |
| \(9.1\) | \(>2.6\) | 21-cm power spectrum | Greig et al. 2021a | |
| \(8.7\) | \(>2.4\) | 21-cm power spectrum | Greig et al. 2021b | |
| \(8.2\) | \(>2.1\) | 21-cm power spectrum | Greig et al. 2021b | |
| \(7.8\) | \(>1.8\) | 21-cm power spectrum | Greig et al. 2021b | |
| \(7.1\) | \(>1.5\) | 21-cm power spectrum | Greig et al. 2021b | |
| \(6.8\) | \(>1.4\) | 21-cm power spectrum | Greig et al. 2021b | |
| \(6.5\) | \(>1.3\) | 21-cm power spectrum | Greig et al. 2021b | |
| \(5.8\pm0.1\) | \(12000\pm2200\) | Ly\(\alpha\) transmission spikes | Gaikwad et al. 2020 | |
| \(5.6\pm0.1\) | \(10500\pm2100\) | Ly\(\alpha\) transmission spikes | Gaikwad et al. 2020 | |
| \(5.4\pm0.1\) | \(11000\pm1600\) | Ly\(\alpha\) transmission spikes | Gaikwad et al. 2020 | |
| \(5.0\) | \(7370^{+1670}_{-1390}\) | Ly\(\alpha\) forest power spectrum | Boera et al. 2019 | |
| \(5.4\) | \(5990^{+1520}_{-1340}\) | Ly\(\alpha\) forest power spectrum | Walther et al. 2019 | |
| \(5.0\) | \(5330^{+1220}_{-910}\) | Ly\(\alpha\) forest power spectrum | Walther et al. 2019 | |
| \(6.08\pm0.33\) | \(5888^{+824}_{-1060}\) | Ly\(\alpha\) absorption lines | Bolton et al. 2012 |
Neutral Hydrogen fraction measurements at \(z\geq5\)
| \(z\) | \(x_{\rm HI}\) | Method | Reference |
|---|---|---|---|
| \(6.55\pm0.05\) | \(<0.18\) | Damping wing | Greig et al. 2024 |
| \(6.35\pm0.05\) | \(0.29^{+0.14}_{-0.13}\) | Damping wing | Greig et al. 2024 |
| \(6.15\pm0.05\) | \(0.20^{+0.14}_{-0.12}\) | Damping wing | Greig et al. 2024 |
| \(6.05\pm0.05\) | \(<0.21\) | Damping wing | Greig et al. 2024 |
| \(5.95\pm0.05\) | \(<0.20\) | Damping wing | Greig et al. 2024 |
| \(5.90\pm0.05\) | \(<0.21\) | Damping wing | Greig et al. 2024 |
| \(6.30\) | \(<0.15\) | Damping wing in GRB | Fausey et al. 2024 |
| \(6.87\) | \(0.37\pm0.17\) | Damping wing | Ďurovčíková et al. 2024 |
| \(6.46\) | \(0.21^{+0.33}_{-0.07}\) | Damping wing | Ďurovčíková et al. 2024 |
| \(6.10\) | \(0.21^{+0.17}_{-0.07}\) | Damping wing | Ďurovčíková et al. 2024 |
| \(6.00\pm0.05\) | \(0.17^{+0.09}_{-0.11}\) | CDF of Ly\(\alpha\) effective optical depth | Gaikwad et al. 2023 |
| \(5.90\pm0.05\) | \(0.13^{+0.13}_{-0.07}\) | CDF of Ly\(\alpha\) effective optical depth | Gaikwad et al. 2023 |
| \(5.80\pm0.05\) | \(0.94^{+0.62}_{-0.64}\times10^{-1}\) | CDF of Ly\(\alpha\) effective optical depth | Gaikwad et al. 2023 |
| \(5.70\pm0.05\) | \(0.56^{+0.71}_{-0.34}\times10^{-1}\) | CDF of Ly\(\alpha\) effective optical depth | Gaikwad et al. 2023 |
| \(5.60\pm0.05\) | \(0.16^{+0.25}_{-0.08}\times10^{-1}\) | CDF of Ly\(\alpha\) effective optical depth | Gaikwad et al. 2023 |
| \(5.50\pm0.05\) | \(0.73^{+2.7}_{-0.35}\times10^{-2}\) | CDF of Ly\(\alpha\) effective optical depth | Gaikwad et al. 2023 |
| \(5.40\pm0.05\) | \(0.35^{+1.5}_{-0.25}\times10^{-2}\) | CDF of Ly\(\alpha\) effective optical depth | Gaikwad et al. 2023 |
| \(5.30\pm0.05\) | \(0.51^{+0.80}_{-0.40}\times10^{-3}\) | CDF of Ly\(\alpha\) effective optical depth | Gaikwad et al. 2023 |
| \(5.20\pm0.05\) | \(0.28^{+0.08}_{-0.06}\times10^{-4}\) | CDF of Ly\(\alpha\) effective optical depth | Gaikwad et al. 2023 |
| \(5.10\pm0.05\) | \(0.27^{+0.13}_{-0.06}\times10^{-4}\) | CDF of Ly\(\alpha\) effective optical depth | Gaikwad et al. 2023 |
| \(5.00\pm0.05\) | \(0.23^{+0.08}_{-0.04}\times10^{-4}\) | CDF of Ly\(\alpha\) effective optical depth | Gaikwad et al. 2023 |
| \(9.80^{+1.60}_{-1.16}\) | \(0.83^{+0.12}_{-0.21}\) | Damping wing | Umeda et al. 2023 |
| \(7.96^{+0.59}_{-0.28}\) | \(0.63^{+0.26}_{-0.36}\) | Damping wing | Umeda et al. 2023 |
| \(7.45^{+0.10}_{-0.25}\) | \(0.54^{+0.32}_{-0.36}\) | Damping wing | Umeda et al. 2023 |
| \(7.14^{+0.04}_{-0.08}\) | \(0.46^{+0.36}_{-0.32}\) | Damping wing | Umeda et al. 2023 |
| \(10.6\) | \(<0.88\) | Ly\(\alpha\) emitting galaxies | Bruton et al. 2023 |
| \(6.70\) | \(<0.94\pm0.06\) | Dark pixel fraction | Jin et al. 2023 |
| \(6.50\) | \(<0.87\pm0.03\) | Dark pixel fraction | Jin et al. 2023 |
| \(6.30\) | \(<0.79\pm0.04\) | Dark pixel fraction | Jin et al. 2023 |
| \(6.90\) | \(<0.33\) | Ly\(\alpha\) emitting galaxies | Wold et al. 2022 |
| \(7.29\) | \(0.49\pm0.11\) | Damping wing | Greig et al. 2022 |
| \(7.60\pm0.6\) | \(0.83^{+0.08}_{-0.11}\) | Lyman break galaxies | Bolan et al. 2022 |
| \(5.95\pm0.2\) | \(<0.29\) | Dark gaps | Zhu et al. 2022 |
| \(5.75\pm0.2\) | \(<0.17\) | Dark gaps | Zhu et al. 2022 |
| \(5.55\pm0.2\) | \(<0.05\) | Dark gaps | Zhu et al. 2022 |
| \(6.70\pm0.2\) | \(<0.25\) | Lyman break galaxies | Bolan et al. 2022 |
| \(7.30\) | \(>0.28\) | Ly\(\alpha\) emitting galaxies | Goto et al. 2021 |
| \(7.30\) | \(0.69\pm0.11\) | Ly\(\alpha\) emitting galaxies | Morales et al. 2021 |
| \(7.00\) | \(0.28\pm0.05\) | Ly\(\alpha\) emitting galaxies | Morales et al. 2021 |
| \(6.60\) | \(0.08^{+0.08}_{-0.05}\) | Ly\(\alpha\) emitting galaxies | Morales et al. 2021 |
| \(7.50\) | \(0.39^{+0.22}_{-0.13}\) | Damping wing | Yang et al. 2020 |
| \(7.00\) | \(0.70^{+0.20,+0.28}_{-0.23,-0.48}\)* | Damping wing | Wang et al. 2020 |
| \(7.90\pm0.6\) | \(>0.46\) | Ly\(\alpha\) emitting galaxies | Mason et al. 2019 |
| \(7.50\) | \(0.21^{+0.17}_{-0.19}\) | Damping wing | Greig et al. 2019 |
| \(7.54\) | \(0.56^{+0.21}_{-0.18}\)** | Damping wing | Bañados et al. 2018 |
| \(7.54\) | \(0.60^{+0.20,+0.36}_{-0.23,-0.45}\)* | Damping wing | Davies et al. 2018 |
| \(7.09\) | \(0.48^{+0.26,+0.47}_{-0.26,-0.46}\)* | Damping wing | Davies et al. 2018 |
| \(7.00\) | \(0.59^{+0.11}_{-0.15}\) | Ly\(\alpha\) emitting galaxies | Mason et al. 2018 |
| \(7.08\) | \(0.40^{+0.21,+0.41}_{-0.19,-0.32}\)* | Damping wing | Greig et al. 2017 |
| \(6.10\) | \(<0.37\) | Dark pixel fraction | McGreer et al. 2015 |
| \(5.90\) | \(<0.06\) | Dark pixel fraction | McGreer et al. 2015 |
| \(5.60\) | \(<0.04\) | Dark pixel fraction | McGreer et al. 2015 |
The uncertainties come from the 68th percentiles. However there are some exceptions:
\(*\) the first uncertainty comes from the 68th percentile while the second value comes from the 95th percentile.
\(**\) the uncertainty comes from the 95th percentile.
The excel file containing this data can be accessed here.
If you know about any data that would be appropriate to add here, please do not hesitate to let me know! Thank you!
Last website update - 08.07.2024